Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые (<90°).

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

1. △ABD ∼ △ABC по двум равным углам: ∠ADB = ∠BAC (прямые), ∠ABD = ∠ABC.

2. △ADC ∼ △ABC по двум равным углам: ∠ADC = ∠BAC (прямые), ∠ACD = ∠ACB.

3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC.
Следовательно, ∠BAD = ∠ACD.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

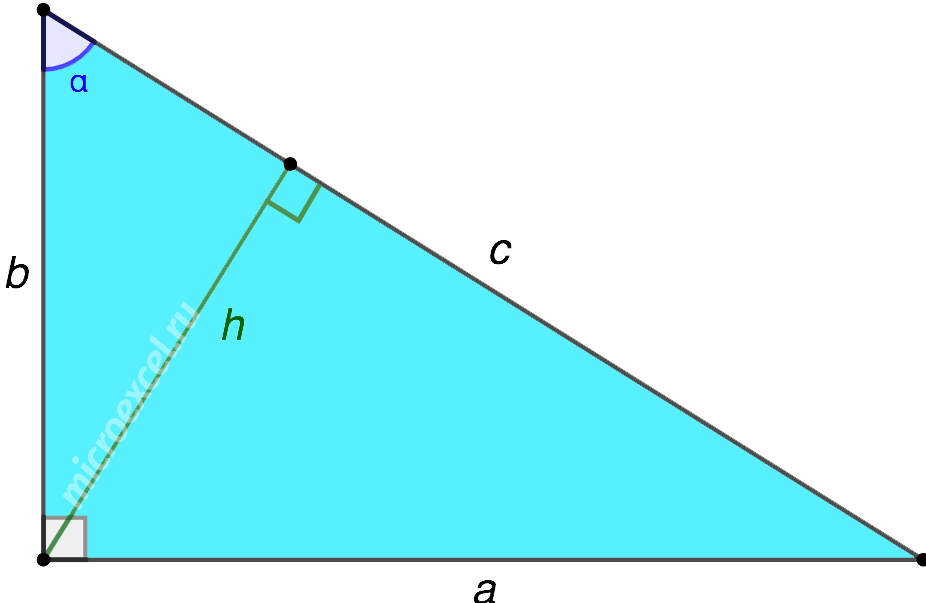
Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c² = a² + b² = 9² + 12² = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше: