В данной публикации мы рассмотрим правила и формулы дифференцирования производной функций, а также, разберем примеры для закрепления изученного материала.
Допустим, даны две функции f (x) и u (x), которые имеют производные в точке x. Тогда для них справедливы следующие формулы:
1. Константа в производной
(c ⋅ f(x))‘ = c ⋅ f ‘(x), где c – константа
Т.е. константу можно вынести за знак производной.
Например: (5x3)‘ = 5 ⋅ (x3)‘
2. Производная суммы/разности
(f(x) ± u(x))‘ = f ‘(x) ± u ‘(x)
Производная суммы/разности двух функций равняется сумме/разности, в которой слагаемыми выступают производные данных функций.
Например: (6x + x2)‘ = (6x)‘ + (x2)‘
3. Производная произведения
(f(x) ⋅ u(x))‘ = f ‘(x) ⋅ u(x) + f(x) ⋅ u ‘(x)
Производная произведения двух функций равняется сумме, в которой:
- первое слагаемое – это произведение производной первой функции на вторую;
- второе слагаемое – все наоборот.
Например: (ln x ⋅ x3)‘ = (ln x)‘ ⋅ x3 + ln x ⋅ (x3)‘
4. Производная частного
Производная деления одной функции на другую находится по следующей формуле:
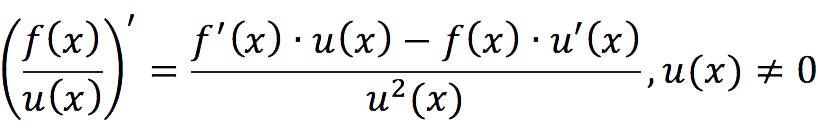
Например:
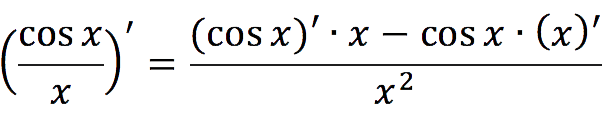
5. Производная сложной функции
Допустим, производная функции y = y(f) находится в точке f0 = f(x0), а функции f = f(x) – в точке x0.
Производная сложной функции в таком случае равняется:
[y(f(x))]‘ = y ‘(f) ⋅ f ‘(x)
- множимое – это производная данной функции по промежуточному аргументу f;
- множитель – производная промежуточного аргумента f по основному аргументу x.



