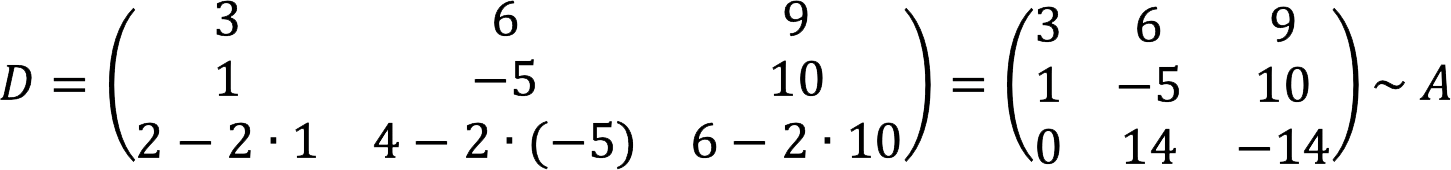В данной публикации мы рассмотрим, что такое элементарные (эквивалентные) преобразования матрицы, какие бывают виды, а также разберем примеры для демонстрации теории на практике.
Определение и виды элементарных преобразований
Элементарными называются такие преобразования матрицы, при которых сохраняется эквивалентность матриц (из-за этого их часто называют эквивалентными). Другими словами такие преобразования не меняют множество решений СЛАУ, которая представлена данной матрицей.
Элементарные преобразования применяются в метода Гаусса, чтобы привести матрицу к треугольному или ступенчатому виду.
К элементарным преобразованиям относятся:
- перестановка двух любых строк местами;
- умножение любой строки на ненулевую константу;
- сумма двух любых строк, одна из которых умножена на определенное ненулевое число.
Примечание: аналогичные действия применимы и к столбцам матрицы.
Матрицы A и B являются эквивалентными, если B получена путем элементарных преобразований A (или наоборот). Для обозначения эквивалентности используется специальный символ – “~“, т.е. A ~ B.
Примеры эквивалентных преобразований матрицы
Давайте на примере матрицы ниже покажем все виды элементарных преобразований.

1. Поменяем вторую и третью строки местами.

2. Умножим первую строку на число 3.

3. Вычтем из третьей строки удвоенную вторую.