Формы записи комплексного числа: тригонометрическая, показательная

В данной публикации рассмотрена тригонометрическая форма комплексного числа с интерпретацией на коордлинатной плоскости, формулами расчета аргумента и примером для лучшего понимания изложенного материала. Также представлена базовая информация по показательной форме данного типа числа.

Тригонометрическая форма комплексного числа

Любое комплексное число (за искл. нуля) вида z = a + bi можно записать в тригонометрической форме следующим образом:

z = |z| ⋅ (cos φ + i ⋅ sin φ)

Чтобы было понятнее, покажем комплексное число на координатной плоскости. При этом, в качестве примера будем исходить из того, что a и b больше нуля.

Модуль комплексного числа |z| – это расстояние от начала координат до соответствующей точки на комплексной плоскости, другими словами, это длина зеленого вектора на чертеже выше.

Исходя из теоремы Пифагора модуль вычисляется так:

Аргумент комплексного числа (φ) – угол между положительной полуосью действительной оси (RE) и вектором, который проведен из начала координат. Аргумент не существует для z = 0, может обозначаться как arg z.

Формула для расчета аргумента зависит от того, какие значения принимают a и b.

a > 0	1-ая и 4-ая координатные четверти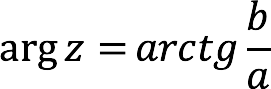
a < 0, b > 0	2-ая координатная четверть
a < 0, b < 0	3-ая координатная плоскость

Пример: представим в тригонометрической форме комплексное число z = 3i.

Решение:
a = 0, b = 3, следовательно:

Т.к. a = 0, значит вектор совпадает с осью ординат (направлен вверх), следовательно φ = 90°.

Таким образом, тригонометрическая форма числа z = 3i выглядит так:
z = 3 ⋅ (cos 90° + i ⋅ sin 90°)

Показательная форма комплексного числа

Любое комплексное число (за искл. нуля) вида z = a + bi можно записать в показательной форме:

z = |z| ⋅ e ^iφ, где:

• |z| – модуль комплексного числа;
• φ – его аргумент.

Примечание: показательная форма используется намного реже, чем тригонометрическая, поэтому базовой информации выше в большинстве случаев должно быть достаточно.