В данной публикации мы рассмотрим определение и свойства одной из основных геометрических фигур – круга. Также приведем формулы, с помощью которых можно найти его радиус, диаметр, периметр и площадь (полную и сектора).
Определение круга
Круг – это множество точек на плоскости, ограниченных окружностью (т.е. лежащих внутри окружности). На рисунке ниже всё, что закрашено бирюзовым цветом, является кругом.

Сектор круга – область внутри круга, которая образована двумя радиусами и дугой между ними.

Сегмент круга – область, образованная в результате деления круга хордой, которая в свою очередь является частью секущей (прямой), пересекающей круг.

- AB – секущая;
- CD – хорда (отрезок, соединяющий две любые точки окружности).
Свойства круга
Свойство 1
Центр круга совпадает с центром ограничивающей его окружности. Чаще всего, обозначается буквой O.
Свойство 2
Радиус круга (R) является, в т.ч., радиусом граничной окружности. Это отрезок, соединяющий центр круга с любой точкой, лежащей на его границе, т.е. на окружности.
Хорда, проходящая через центр круга называется его диаметром (d).

Свойство 3
Периметр круга равняется длине ограничивающей его окружности.
Свойство 4
Круг по сравнению с другими фигурами имеет наибольшую площадь при заданном периметре.
Формулы
1. Периметр круга (L):
![]()
2. Радиус круга (R):
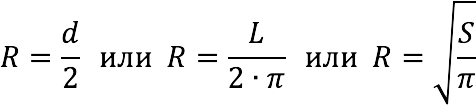
3. Диаметр круга (d):

4. Площадь круга (S):
![]()
5. Площадь сектора (S):
![]()



