Решение неравенств с модулем

В данной публикации мы рассмотрим, что из себя представляют неравенства с модулем (одним или двумя), а также на практических примерах покажем, как их решать.

Примечание: что такое модуль числа, мы рассмотрели в отдельной публикации.

Внешний вид неравенств

Неравенства с одним модулем выглядят следующим образом:

• |x| > 5
  (модуль икс больше 5)
• |x – 7| < 4
  (модуль икс минус 7 меньше 4)
• |x + 2| ≥ 11
  (модуль икс плюс 2 больше или равен 11)

В модуле указывается неизвестная переменная x или выражение с ней.

Решение неравенств

Разберем по порядку решение представленных выше примеров.

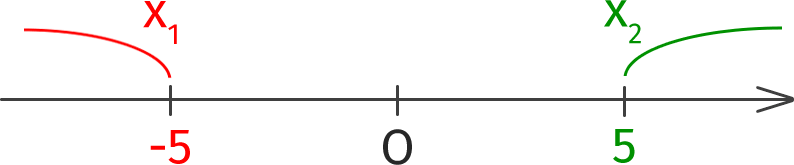
|x| > 5

Это следует понимать таким образом: на числовой оси существуют такие точки, расстояние от которых до нуля больше пяти. Т.е. это точки больше 5 или меньше -5, следовательно, у данного неравенства два решения: x₁ ∈ (-∞; -5) и x₂ ∈ (5; ∞).

|x – 7| < 4

Т.е. на числовой линейке существует такое множество точек x, расстояние от которых до точки 7 меньше 4. Следовательно, неравенство имеет следующее решение:
7 – 4 < x < 7 + 4 или x ∈ (3; 11).

|x + 2| ≥ 11

Данное неравенство можно представить в таком виде: |x – (-2)| ≥ 11.

Таким образом, на числовой оси точки x находятся на расстоянии не менее 11 от точки -2. Значит:

• x₁  ≥ 9 (-2 + 11) или x₁ ∈ [9; ∞)
• x₂ ≤ -13 (-2 – 11) или x₂ ∈ (-∞; -13]

Примечание:

Некоторые неравенства могут содержать два модуля: например: |x| > |y|.
Для него, также, есть два решения: x₁ ∈ (-∞; -y) и x₂ ∈ (y; ∞).