Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.
Формула вычисления площади
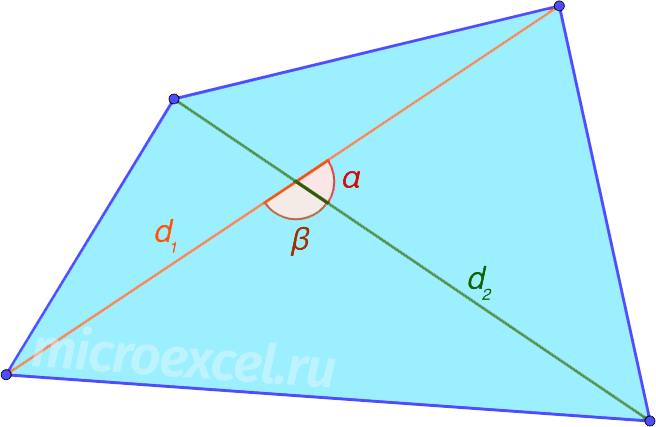
По диагоналям и углу между ними
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.
![]()
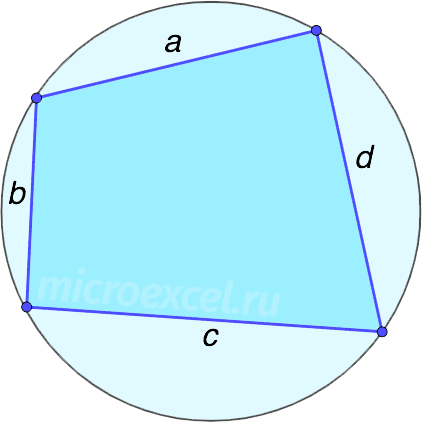
По четырем сторонам (формула Брахмагупты)
Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.
![]()
p – полупериметр, вычисляется следующим образом:
![]()
По радиусу вписанной окружности и сторонам
Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:
S = p ⋅ r

r – радиус окружности.
Пример задачи
Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.
Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см2.



