Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

• m – количество уравнений;
• n – количество переменных.
• x₁, x₂,…, x_n – неизвестные;
• a₁₁, a₁₂,…, a_mn – коэффициенты при неизвестных;
• b₁, b₂,…, b_m – свободные члены.

Индексы коэффициентов (a_ij) формируются следующим образом:

• i – номер линейного уравнения;
• j – номер переменной, к которой относится коэффициент.

Решение СЛАУ – такие числа c₁, c₂,…, c_n , при постановке которых вместо x₁, x₂,…, x_n, все уравнения системы превратятся в тождества.

Виды СЛАУ

1. Однородная – все свободные члены системы равны нулю (b₁ = b₂ = … = b_m = 0).
   
2. Неоднородная – если не выполняется условие выше.
3. Квадратная – количество уравнений равно числу неизвестных, т.е. m = n.
   
4. Недоопределенная – число неизвестных больше количества уравнений.
   
5. Переопределенная – уравнений больше, чем переменных.
   

В зависимости от количества решений, СЛАУ может быть:

1. Совместная – имеет хотя бы одно решение. При этом если оно единственное, система называется определенной, если решений несколько – неопределенной.
   
   СЛАУ выше является совместной, т.к. есть хотя бы одно решение: x = 2, y = 3.
2. Несовместная – система не имеет решений.
   
   Правые части уравнений одинаковые, а левые – нет. Таким образом, решений нет.

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

AX = B

• A – матрица, которая образована коэффициентами при неизвестных:
  
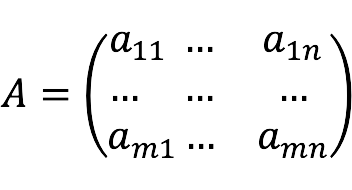
• X – столбец переменных:
  
• B – столбец свободных членов:
  

Пример
Представим систему уравнений ниже в матричном виде:

Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

Полная запись заданной системы уравнений в матричном виде:

Расширенная матрица СЛАУ

Если к матрице системы A добавить справа столбец свободных членов B, разделив данные вертикальной чертой, то получится расширенная матрица СЛАУ.

Для примера выше получается так:

– обозначение расширенной матрицы.