В данной публикации мы рассмотрим теорему Виета, определяющую взаимосвязи между коэффициентами многочлена и его корнями, а также, научимся применять ее на практике для решения задач.
Формулировка теоремы
Если c1, c2…, cn являются корнями многочлена xn + a1xn−1 + a2xn−2 + … + an, где каждый корень взят соответствующее его кратности число раз, то:
коэффициенты a1, a2…, an можно выразить в виде симметрических многочленов от корней, т.е.:
- a1 = −(c1 + c2 + … + cn)
- a2 = c1c2 + c1c3 + … + c1cn + c2c3 + … + cn−1cn
- a3 = −(c1c2c3 + c1c2c4 + … + cn−2cn−1cn)
- an−1 = (−1)n−1(c1c2 … cn−1 + c1c2 … cn−2cn + … + c2c3 … cn
- an = (−1)nc1c2 … cn
Другими словами, (−1)kak равняется сумме всех возможных произведений из k корней.
Примечание: теорема названа в честь французского маетиматика Франсуа Виета.
Квадратное уравнение
Для квадратного уравнения ax2 + bx + c = 0 с корнями x1 и x2 справедливо:
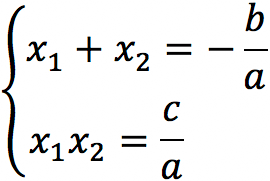
Если уравнение имеет вид x2 + px + c = 0 (приведенная форма при a = 1), то:
![]()
Кубическое уравнение
Для кубического уравнения p(x) = ax3 + bx2 + cx + d = 0 с корнями x1, x2 и x3 справедливо:

Обратная теорема
Если для чисел x1 и x2 справедливы соотношения x1 + x2 = −p, а x1x2 = q, значит они являются корнями приведенного квадратного уравнения x2 + px + c = 0.
Примеры задач
Задание 1
Дано квадратное уравнение x2 − 70x + 600 = 0. Найдите его корни, используя теорему Виета.
Решение:
Используем соотношение корней для приведенного уравнения (т.к. a = 1):
x1 + x2 = 70
x1x2 = 600
Остается только подобрать числа x1 и x2, которые будут одновременно соответствовать данным уравнениям. В нашем случае – это 10 и 60.
Задание 2
Составьте уравнение, если известно, что его корни x1 и x2 равны 2 и −6, соответственно.
Решение:
Допустим, что у нас приведенное квадратное уравнение вида x2 + px + c = 0. В этом случае, исходя из установленных для него соотношений корней получаем:
p = −(x1 + x2) = −(2 + (−6)) = 4
q = x1x2 = 2 ⋅ (−6) = −12
Получаем уравнение, подставив найденные значения в формулу общего вида: x2 + 4x − 12 = 0.



