Теорема о трех перпендикулярах

В данной публикации мы рассмотрим одну из основных теорем в геометрии, изучаемую в 10-11 классах – о трех перпендикулярах. Также разберем пример решения задачи для закрепления изложенного материала.

Формулировка теоремы

Если через основание наклонной на плоскости провести прямую перпендикулярно ее проекции, то данная прямая будет перпендикулярна и самой наклонной.

• α – плоскость;
• a – наклонная;
• b – проекция наклонной (a) на плоскости (α);
• с – прямая на плоскости (α), перпендикулярная проекции наклонной (b).

Обратная теорема

Если через основание наклонной на плоскости провести перпендикулярную ей прямую, то данная прямая будет перпендикулярна и проекции наклонной на плоскости.

Пример задачи

Длина наклонной, проведенной из точки A к плоскости α, равна 10 см, а ее проекции – 6 см. Найдите расстояние точки A до плоскости.

Решение
Нарисуем условие задачи в виде чертежа ниже.

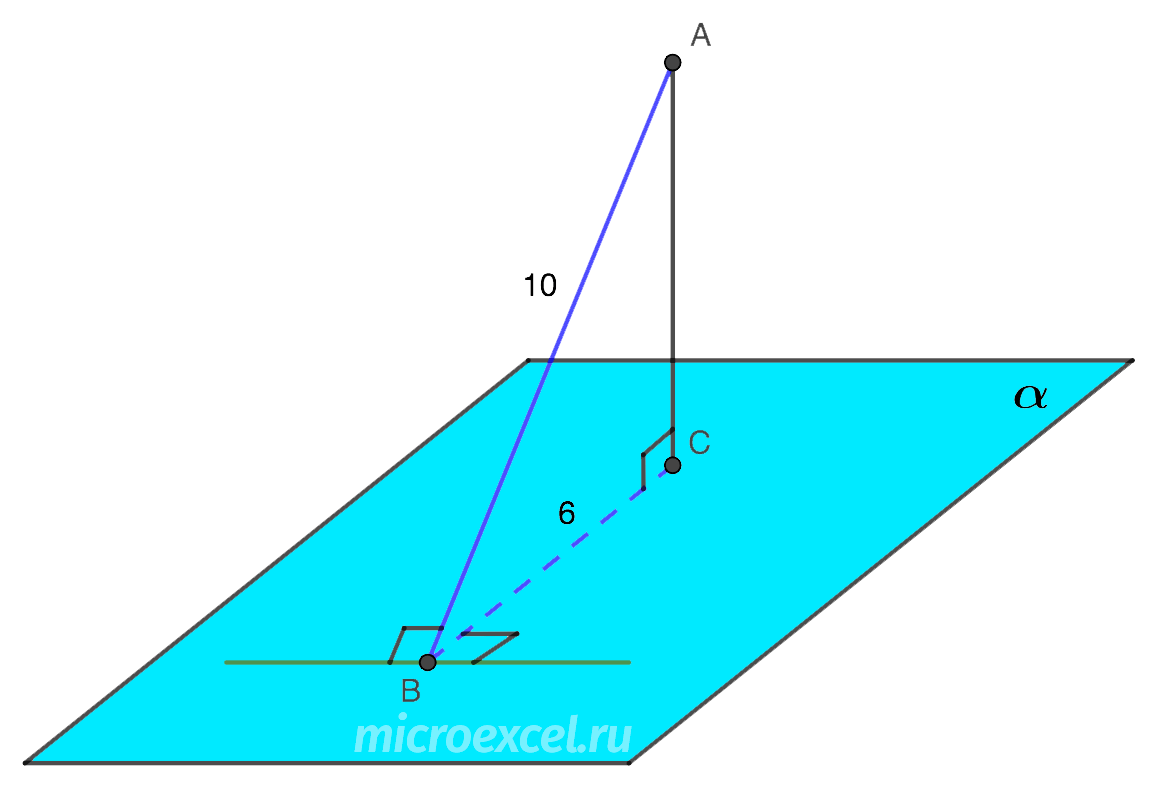
Расстояние от точки A до плоскости α – это длина отрезка AC, который одновременно является катетом прямоугольного треугольника ABC.

Воспользовавшись теоремой Пифагора получаем:

AC² = AB² – BC² = 10² – 6² = 64.
Следовательно, AC = √64 = 8 см.