В данной публикации мы рассмотрим, что из себя представляют уравнения с модулем (в т.ч. с двумя), а также продемонстрируем, как их можно решить на практических примерах.
Примечание: что такое модуль числа, мы рассмотрели в отдельной публикации.
Внешний вид уравнений
Уравнения с модулем могут выглядеть примерно следующим образом:
- |x| = 6
(модуль икс равняется 6) - |x – 11| = 3
(модуль икс минус 11 равно 3) - |x + 4| = 9
(модуль икс плюс 4 равняется 9)
Т.е. в модуле указана неизвестная переменная (просто x или выражение, включающее x).
Решение уравнений
Давайте разберем решение каждого из перечисленных выше примеров.
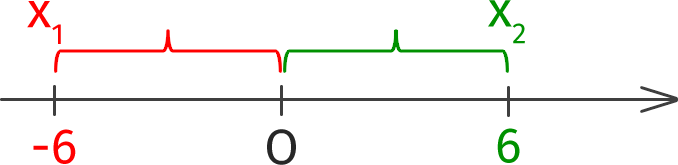
|x| = 6
Это означает, что на числовой оси есть две точки, расстояние от которых до нуля равняется шести. Т.е. это точки -6 и 6, следовательно, у данного уравнения два корня:
|x – 11| = 3
В данном случае на числовой оси расстояние от точки x до точки 11 равняется 3. Таким образом, уравнение имеет два корня:

|x + 4| = 9
Это уравнение можно переписать следующим образом: |x – (-4)| = 9.
Теперь мы можем его интерпретировать так: на координатной оси точка x находится на расстоянии 9 от точки -4. Значит,
Примечание:
Иногда могут встречаться уравнения с двумя модулями, например: |x| = |y|.
В данном случае, также существуют два корня:



