Что такое эллипс: определение, основные элементы, уравнение

В данной публикации мы рассмотрим определение, основные элементы и уравнения (каноническое и параметрическое) одной из основных геометрических фигур – эллипса.

Определение эллипса

Эллипс – это замкнутая кривая на плоскости, сумма расстояний от каждой точки которой до ее фокусов (F₁ и F₂) равна постоянному значению.

F₁M₁ + F₂M₁ = F₁M₂ + F₂M₂ = A₁A₂ = const

Примечание: частным случаем эллипса является окружность.

Элементы эллипса

Для рисунка выше:

• F₁ и F₂ – фокусы эллипса;
• A₁A₂ – большая ось эллипса, проходит через его фокусы;
• B₁B₂ – малая ось эллипса, перпендикулярна большей оси и проходит через ее центр;
• A₁O = OA₂ = a – большая полуось эллипса;
• B₁O = OB₂ = b – малая полуось эллипса;
• точка O – центр эллипса, является пересечением большой и малой осей фигуры;
• A₁, A₂, B₁, B₂ – вершины эллипса, точки пересечения кривой с осями.
• Радиус эллипса (R) – отрезок, соединяющий центр фигуры с точкой на ее кривой (в формуле ниже φ – это угол между радиусом и большой осью).
• Диаметр эллипса (d) – отрезок, который проходит через центр фигуры и соединяет две противоположные точки на ее кривой.
• Фокальное расстояние (c) – половина отрезка, соединяющего фокусы эллипса.
• Фокальные радиусы эллипса (r₁ и r₂) – отрезки, которые соединяют фокусы с точкой на кривой.
• r_a – перифокусное расстояние (минимальное расстояние от фокуса до точки на кривой эллипса);
• r_b – апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
• Эксцентриситет эллипсa (e) – растяженность фигуры, характеризуется отношением фокального расстояния к большей полуоси.
• Фокальный параметр эллипса (p) – отрезок, который соединяет фокус фигуры и точку на кривой, перпендикулярен ее большей полуоси.
• Коэффициент сжатия эллипса (k) – определяется отношением малой полуоси к большой. Также называется эллиптичностью фигуры.
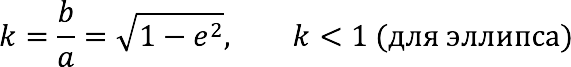
• Сжатие эллипса (1 – k) – разность между единицей и эллиптичностью.

Примечание: свойства эллипса представлены в отдельной публикации.

Уравнение эллипса

Каноническое уравнение эллипса

Если центр эллипса (точка O) находится в начале системы координат (декартовой), а большая ось лежит на оси абсцисс, то фигуру можно описать уравнением ниже:

Если центр эллипса находится в точке с координатами (x₀; y₀), уравнение принимает следующий вид:

Параметрическое уравнение эллипса

Для параметра α: