Деление комплексных чисел

В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.

Деление в алгебраической форме

Результатом деления (т.е. частное) двух комплексных чисел x = a₁ + b₁i и y = a₂ + b₂i также является комплексное число z:

Порядок действий следующий:

1. Делимое и делитель умножаем на число, комплексно сопряженное делителю. Не забываем, что i² = -1.
   
   Примечание: Для (a + bi) комплексно сопряженным будет число (a – bi), т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный.
2. В результате выполнения умножения в знаменателе получается обычное действительное число.
   (a₂ + b₂i)(a₂ – b₂i) = a₂ ⋅ a₂ – a₂ ⋅ b₂i + b₂i ⋅ a₂ – b₂i ⋅ b₂i = a₂² – b₂² ⋅ i² = a₂² + b₂².
3. Теперь выполним аналогичное действие в числителе:
   (a₁ + b₁i)(a₂ – b₂i) = a₁ ⋅ a₂ – a₁ ⋅ b₂i + b₁i ⋅ a₂ – b₁i ⋅ b₂i = a₁a₂ – b₁b₂i² – a₁b₂i + b₁a₂i = (a₁a₂ + b₁b₂) + (a₂b₁ – a₁b₂) ⋅ i.
4. Делим полученный числитель на знаменатель:
   

Пример 1:
Разделим комплексное число (3 – i) на (-5 + 2i).

Решение:
Руководствуемся планом действий, описанным выше, и получаем:

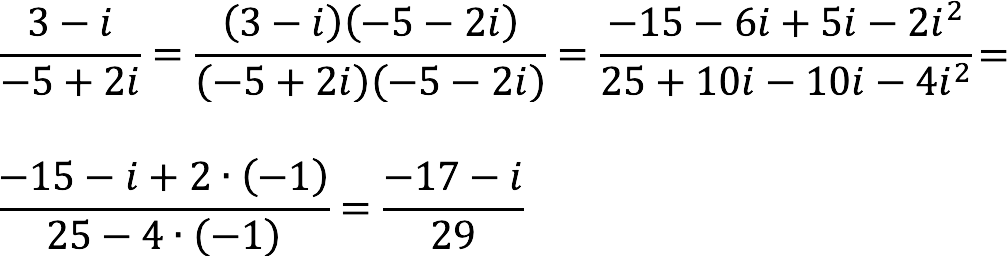
Деление в геометрической форме

Если комплексные числа заданы в тригонометрической форме, например, x = |x| ⋅ (cos φ₁ + i ⋅ sin φ₁) и y = |y| ⋅ (cos φ₂ + i ⋅ sin φ₂), то разделить их можно по формуле ниже:

Пример 2
Найдем частное комплексных чисел: x = 4 ⋅ (cos 60° + i ⋅ sin 60°) и y = 2 ⋅ (cos 25° + i ⋅ sin 25°).

Решение:
|x| : |y| = 4 : 2 = 2
φ₁ – φ₂ = 60° – 25° = 35°
x : y = 2 ⋅ (cos 35° + i ⋅ sin 35°)