В данной публикации мы рассмотрим, какие виды матриц существуют, сопроводив их практическими примерами для демонстрации изложенного теоретического материала.
Напомним, что матрица – это некая прямоугольная таблица, состоящая из столбцов и строк, которые заполнены определенными элементами.
Виды матриц
1. Если матрица состоит из одной строки, она называется вектор-строкой (или матрицей-строкой).
Пример:
![]()
2. Матрица, состоящая из одного столбца, называется вектором-столбцом (или матрицей-столбцом).
Пример:

3. Квадратная – матрица, которая содержит одинаковое количество строк и столбцов, т.е. m (строки) равняется n (столбцы). Размер матрицы можно задать как n x n или m x m, где m (n) – ее порядок.
Пример:
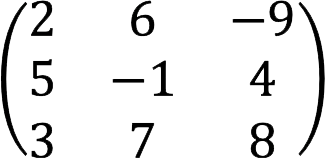
4. Нулевая – матрица, все элементы которой равняются нулю (aij = 0).
Пример:

5. Диагональная – квадратная матрица, у которой все элементы, за исключением расположенных на главной диагонали, равняются нулю. Одновременно является верхней и нижней треугольной.
Пример:

6. Единичная – это разновидность диагональной матрицы, у которой все элементы главной диагонали равны единице. Обычно обозначается буквой E.
Пример:

7. Верхняя треугольная – все элементы матрицы ниже главной диагонали равны нулю.
Пример:

8. Нижняя треугольная – матрица, все элементы которой выше главной диагонали равняются нулю.
Пример:

9. Ступенчатая – матрица, для которой выполняются следующие условия:
- если в матрице есть нулевая строка, то все остальные строки, находящиеся под ней, являются нулевыми.
- если первый ненулевой элемент определенной строки находится в столбце с порядковым номером j, и следующая строка является ненулевой, то первый ненулевой элемент следущей строки должен располагаться в столбце с номером больше, чем j.
Пример:




